Contoh Soal Persamaan Logaritma – Dalam operasi matematika, ada banyak operasi yang memiliki pasangan berkebalikan. Misalnya seperti, penjumlahan dengan pengurangan, perkalian dan pembagian, serta logaritma dengan eksponen dan masih banyak lagi yang lainnya.
Nah, berbicara soal logaritma sendiri, tentunya anda semuanya sudah tidak asing lagi dengan materi pelajaran matematika yang satu ini. Materi dasar matematika logaritma ini muncul pada operasi matematika dasar yaitu perpangkatan bilangan.
Perkembangan ilmu matematika yang semakin pesat, membuat materi ini bukan hanya sebatas hitung menghitung saja. Namun, perkembangan ilmu ini juga terjadi berdasarkan pada penalaran-penalaran yang logis dan sistematis.
Dalam kehidupan nyata, logaritma banyak digunakan untuk memecahkan sebuah persamaan perpangkatan yang belum diketahui. Hal inilah yang membuat logaritma menjadi ilmu yang sangat penting. Untuk informasi yang lebih jelasnya, simak ulasan di bawah ini.
Kumpulan Soal Persamaan Logaritma Lengkap

Nah, sebagai penjelasan pemahaman anda dalam perhitungan logaritma, di sini inspired2write akan sajikan beberapa contoh soal persamaan logaritma lengkap dengan penjelasannya. Maka dari itu, bagi yang masih bingung dengan perhitungan persamaan logaritma, silahkan simak ulasan di bawah ini.
Materi Logaritma

A. Pengertian Logaritma
Logaritma adalah operasi matematika kebalikan atau invers dari pemangkatan.
ab = c ⇔ alog c = b dengan syarat x > 0, a > 0 dan a ≠ 1.
Pada rumus di atas, a yaitu basis atau pokok utama dari logaritma tersebut.
Persamaan logaritma adalah sebuah persamaan yang peubahnya ada dalam bilangan pokok (numerus) logaritma.
B. Sifat Logaritma
Adapun sifat-sifat logaritma, silahkan simak tabel di bawah ini.
| alog a = 1 |
| alog 1 = 0 |
| alog an = n |
| alog bn = n • alog b |
| alog b kali c = alog b ditambah alog c |
| alog b/c = alog b – alog c |
| aˆnlog bm = m/n • alog b |
| alog b = 1 ÷ blog a |
| alog a • blog c • clog d = alog d |
| alog b = clog b ÷ clog a |
C. Sifat Persamaan Logaritma
Sedangkan untuk sifat-sifat persamaan logaritma yaitu sebagai berikut.
1. Sifat Logaritma Dari Perkalian
Hasil penjumlahan dari 2 bilangan logaritma yang nilai bilangan pokok keduanya merupakan faktor dari nilai pokok awal.
alog p. q = alog p + alog q
Dengan syarat : a>0, a\ne 1 dan p>0 serta q>0
2. Perkalian Logaritma
Sifat logaritma a dikalikan dengan logaritma b, jika nilai bilangan pokok logaritma a = b.
alog b × blog c = alog c
Dengan syarat : a>0 dan a \ne 1
3. Sifat Logaritma dari Pembagian
Hasil pengurangan 2 bilangan logaritma yang nilai bilangan pokok keduanya yaitu pecahan atau pembagian dari nilai numerus awal.
alog p/q : alog p – alog q
Dengan syarat : a>0, a \ne 1, p>0 dan 1>0
4. Sifat Logaritma Berbanding Terbalik
Suatu sifat logaritma lain yang memiliki nilai numerus saling bertukaran.
alog b = 1/blog a
Dengan syarat : a>0 dan a \ne 1
5. Logaritma Berlawanan Tanda
Sifat logaritma yang memiliki nilai pokok dengan pecahan berbanding terbalik dari numerus logaritma awal.
alog p/q = – alog p/q
Dengan syarat : a>0, a \ne 1, p>0 dan q>0
6. Sifat Logaritma Dari Perpangkatan
Suatu sifat logaritma yang nilai numerusnya berupa eksponen yang dapat dijadikan sebagai logaritma baru dengan mengeluarkan pengkat menjadi bilangan pengali.
alog bp = p × alog b
Dengan syarat : a>0, a \ne 1 dan b>0
7. Perpangkatan Bilangan Pokok Logaritma
Nilai bilangan pokok suatu eksponen yang bisa dijadikan logaritma baru dengan mengeluarkan pangkat sebagai bilangan pengali.
aplog b = 1/palog b
Dengan syarat : a>0 dan a \ne 1
8. Bilangan Pokok Logaritma Sebanding Dengan Perpangkatan Numerus
Nilai pokok suatu pangkat dari nilai bilangan pokok yang memiliki hasil yang sama dengan nilai pangkat bilangan pokok.
alog ap = p
Dengan syarat : a>0 dan a\ne 1
9. Perpangkatan Logaritma
Sifat bilangan yang memiliki pangkat yang dilogaritma dan hasil perpangkatannya berupa nilai numerus dari logaritma tersebut.
a alog m = m
Dengan syarat : a>0, a \ne 1 dan m>0
10. Mengubah Basis Logaritma
Logaritma yang dapat dipecah menjadi dua bilangan logaritma.
plog q = alog p / alog q
Dengan syarat : a>0, a \ne 1, p>0 dan q>0
D. Kegunaan Logaritma
Logaritma biasa digunakan untuk memecahkan persamaan bilangan yang pangkatnya tidak diketahui. Turunannya yang mudah dicari, membuat logaritma sering digunakan sebagai salah satu solusi integral. Dalam persamaan { bn = x } b dapat dicari dengan pengakaran, n dicari dengan logaritma dan x dengan fungsi eksponen. Adapun kegunaan logaritma lainnya yaitu sebagai berikut.
a). Sains dan Teknik
- Nilai negatif dari logaritma berbasis 10 digunakan pada ilmu kimia untuk mengekspresikan konsentrasi ion hidronium (pH). Contoh : konsentrasi ion hidronium pada air yaitu 10-7 pada suhu 25 derajat Celcius, sehingga nilai pH = 7
- Satuan bel (B) merupakan satuan pengukuran perbandingan (rasio). Biasanya digunakan dalam bidang telekomunikasi, elektronik serta akustik. Hal ini disebabkan telinga manusia mempersepsikan suara yang terdengar secara logaritma.
- Skala logaritma berbasis 10 juga digunakan untuk mengukur intensitas gempa bumi skala Richter
- Sedangkan dalam astronomi, skala logaritma digunakan untuk menghitung magnitudo yang mengukur terangnya bintang, pasalnya mata manusia mempersepsikan terang secara logaritmik.
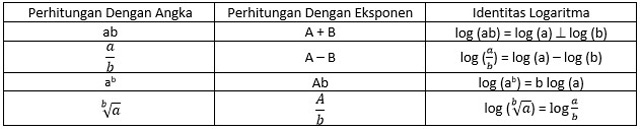
b). Penghitungan Yang Lebih Mudah
Logaritma memindahkan fokus perhitungan dari suatu bilangan normal ke pangkat-pangkat. Apabila basis logaritma sama, maka beberapa jenis penghitungan akan lebih mudah menggunakan logaritma.
c). Kalkulus
Turunan fungsi logaritma yaitu :
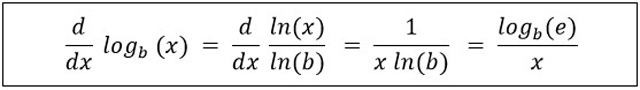
Pada rumus di atas ln yaitu logaritma natural yang merupakan logaritma berbasis e. Apabila b = e, maka rumus di atas dapat disederhanakan seperti berikut.
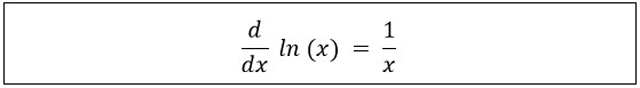
Sedangkan, untuk integral fungsi logaritma yaitu sebagai berikut :
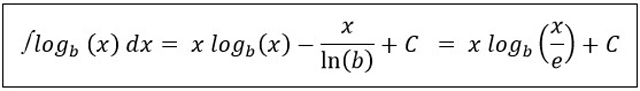
Dan untuk integral logaritma berbasis e yaitu :
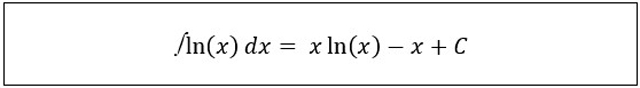
E. Fungsi Logaritma
Fungsi logaritma merupakan fungsi balikan dari fungsi pemangkatan. Jika fungsi pemangkatan dinyatakan dengan f(x) = ax, a>0, a ≠ 1, maka balikan dari f(x0) ditulis f-1(x) = alog x atau f(x) = alog x, a>0, a ≠ 1.
Sehingga secara umumnya, jika y = ax, maka x = alog y.
- Jika f(x) = alog x, dengan syarat a>1, x<0, x e R, maka f(x) dikatakan sebagai fungsi.
- Dan, jika f(x) = alog x, dengan syarat 0<a<1, x>0, x e R, maka f(x) dinyatakan fungsi naik.
Rumus Logaritma

Sedangkan, untuk rumus logaritma sendiri yaitu sebagai berikut :
| Rumus Dasar Logaritma : ab = c ⇔ alog c = b |
| Rumus Logaritma : ac = b → alog b = c |
- a : basis
- b : bilangan logaritma
- c : hasil logaritma
Adapun untuk rumus yang lainnya, sudah kami sajikan pada informasi di atas pada setiap poin artikel ini.
Contoh Soal Persamaan Logaritma
Setelah mengetahui, informasi terkait persamaan logaritma secara coba terapkan rumus di atas dengan contoh soal sebagai berikut :
Contoh Soal I :
Himpunan penyelesaian dari persamaan 2log (x2 – 2x + 1) = 2log (2x2 – 2), maka persamaan logaritma tersebut adalah…
a). -3
b). -2
c). 0
d). 2
e). 3
Jawab :
- x2 -2x + 1 = 2 x2 – 2
- 0 = 2 x2 – 2 – x2 + 2x – 1
- x2 + 2x – 3 = 0
- (x + 3)(x – 1) = 0 ⇔ maka x = -3 dan atau x = 1
Maka hasilnya adalah x = -3, sehingga jawabannya a.
Alasannya yaitu log f(x), syaratnya yaitu f(x)>0. Untuk x = 1 → f(x) 0 tidak berlaku. Maka hasilnya adalah x = -3
Contoh Soal II :
Nilai dari log (9x+4)½ – log 81x-5 = 0, maka nilai x yang tepat pada persamaan di atas yaitu…
a). 4
b). 2
c). 10
d). 8
e). 14
Jawab :
log (9x+4)½ – log 81x-5 = 0
- log (9x+4)½ = log 81x-5
- (32)x+4/2 = (34)x-5
- (3)2.x+4/2 = (3)4(x-5)
- 3x+4 = 34x-20
- x + 4 = 4x – 20
- 3x = 24
- x = 24 ÷ 3
- x = 8
- maka jawabanya adalah : d). 8
Download Contoh Soal Persamaan Logaritma
Untuk contoh soal lainnya, silahkan download contoh soalnya pada link di bawah ini.
Link Download : KUMPULAN CONTOH SOAL PERSAMAAN LOGARITMA DOC.
Link Download : CONTOH SOAL PERSAMAAN LOGARITMA DAN PEMBAHASANYA PDF.
Itulah beberapa contoh soal persamaan logaritma yang dapat inspired2write.com sajikan untuk anda. Dengan mencermati dan mempelajari informasi di atas, maka ujian atau tugas matematika yang dilakukan secara online di Google classroom akan lebih mudah dikerjakan tanpa harus mencontek. Namun, pastikan anda sudah tahu caranya MENGISI TUGAS DI GOOGLE CLASSROOM. Demikian informasi yang dapat inspired2write sajikan, semoga informasi di atas bermanfaat.