Inspired2Write.com – Beberapa contoh soal SPLTV beserta jawabannya akan membantu kita dalam memahami Matematika khususnya bagi kalian yang saat ini duduk di kelas 10. Lantas, apa itu SPLTV dan bagaimana cara menyelesaikan soalnya?
SPLTV adalah anonim dari Sistem Persamaan Linear Tiga Variabel, yaitu X, Y, dan Z. Sistem Persamaan Linear sebenarnya sudah pernah kalian terima saat SMP hanya saja terdiri dari 2 variabel. Gambaran lengkapnya ada di contoh soal SPLTV beserta jawabannya.
Nantinya dalam pembahasan mengenai contoh soal SPLTV beserta jawabannya ini juga akan diberikan materi sebagai pondasi keilmuan dan juga studi kasus. Jadi, bagaimana bentuk contoh soal dari SPLTV tersebut?
Agar dapat membantu kalian yang saat ini ingin mendapatkan Contoh Soal SPLTV beserta jawabannya, maka Inspired2Write akan coba berikan semua referensinya. Jadi simak semua pembahasan supaya lebih mudah dalam menyelesaikan semua persoalannya.
Contoh SPLTV dalam Kehidupan Sehari-hari

Dalam kehidupan sehari-hari, kita biasa menjumpai SPLTV dalam beberapa kasus. Misalkan saja seorang pedagang buah yang ingin memenuhi kiosnya dengan aneka ragam buah-buahan. Namun karena keterbatasan modal, maka pembelian persediaan dilakukan secara bertahap.
Dihari pertama, Si Pedagang berhasil mengumpulkan modal sebanyak Rp. 2.640.000,00. Modal hari pertama tersebut dibelikan beberapa persediaan buah seperti Nanas 3 Dus, Pisan 2 Dus, dan Mangga 5 Dus.
Dihari kedua, Si Pedagang berhasil mengumpulkan modal sebanyak Rp. 1.510.000,00. Modal hari kedua dibelikan beberapa persediaan lagi seperti Nanas 1 Dus, Pisang 5 Dus, dan Mangga 2 Dus.
Sementara dihari ketiga, Si Pedagang berhasil mengumpulkan modal lagi sebanyak Rp. 2.750.000,00. Kemudian modal tersebut dibelikan persediaan berupa Nanas 4 Dus, Pisang 5 Dus, dan Mangga 3 Dus.
Apabila melihat aktivitas pembelian dari Pedagang tersebut, maka kita hanya mengetahui jumlah dus pembeliannya dan belum mengetahui harga untuk satu Dus dari masing-masing buah. Supaya bisa mengetahuinya, maka kita dapat menentukan variabel dengan data sebagai berikut.
- Harga Nanas per Dus = x
- Harga Pisang per Dus = y
- Harga Mangga per Dus = z
Berdasarkan variabel di atas, maka akan tercipta SPLTV (Sistem Persamaan Linear Tiga Variabel) sebagai berikut.
- Hari Pertama : 3x + 2y + 5z = Rp. 2.640.000,00…. (Persamaan 1)
- Hari Kedua : 1x + 5y + 2z = Rp. 1.510.000,00…… (Persamaan 2)
- Hari Ketiga : 4x + 5y + 3z = Rp. 2.750.000,00…. (Persamaan 3)
Ternyata membuat SPLTV berdasarkan kehidupan sehari-hari sangat mudah bukan? Dengan menggunakan Contoh SPLTV tadi, maka kita dapat menemukan harga per dus dari masing-masing persediaan buah.
Bentuk Umum SPLTV (Sistem Persamaan Linear Tiga Variabel) dalam Matematika
Mengacu pada contoh di atas, maka kita dapat menyimpulkan jika SPLTV ternyata memiliki bentuk umum. Nantinya bentuk umum dari SPLTV ini akan sering digunakan dalam beberapa contoh soal. Jadi silahkan pahami terlebih dahulu sebelum melangkah pada contoh soal beserta jawabannya.
Berikut bentuk umum SPLTV (Sistem Persamaan Linear Tiga Variabel) mengacu pada contoh di atas.
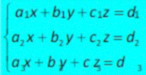
Metode (Cara) Menyelesaikan SPLTV (Sistem Persamaan Linear Tiga Variabel)
SPLTV ada untuk menyelesaikan permasalahan kehidupan sehari-hari. Tentunya dalam proses penyelesaian SPLTV, ada beberapa metode atau cara yang bisa kalian gunakan. Jadi kita tidak akan menebak masing-masing angka dari variabel, melainkan menggunakan sebuah metode.
Berikut beberapa metode (cara) untuk menyelesaikan soal SPLTV (Sistem Persamaan Linear Tiga Variabel).
1. Penyelesaian Soal SPLTV Metode Subtitusi
Penyelesaian SPLTV (dalam variabel x, y, dan z) dengan menggunakan metode subtitusi dapat dilakukan dengan langkah-langkah berikut ini.
- Silahkan pilih salah satu persamaan yang paling sederhan, kemudian nyatakan x sebagai fungsi y dan z; atau y sebagai fungsi x dan z; atau z sebagai fungsi x dan y.
- Subtitusikan x atau y atau z yang sudah didapatkan dengan menggunakan langkah pertama ke dua persamaan lainnya, sehingga akan tercipta Sistem Persamaan Linear Dua Variabel (SPLDV).
- Silahkan hitung terlebih dahulu SPLDV yang sudah didapatkan dengan menggunakan langkah kedua.
- Substitusikan dua nilai variabel yang sudah didapatkan menggunakan langkah ketiga ke salah satu persamaan semula untuk memperoleh nilai variabel ketiga.
Agar langkah-langkah di atas dapat lebih mudah dipahami, maka berikut contoh soal dari penyelesaian SPLTV dengan menggunakan metode Substitusi.
x + y + z = 0 (Contoh Bentuk Persamaan 1)
x – y + z = 4 (Contoh Bentuk Persamaan 2)
3x + 2y + z = 2 (Contoh Bentuk Persamaan 3)
Jawabannya:
Persamaan kedua silahkan diubah menjadi x = 4 + y – z dan terciptalah persamaan keempat (4). Kemudian subtitusikan persamaan keempat (4) ke persamaan (1).
- Sebelum: x + y + 2z = 0
- Sesudah: (4 + y – z) + y – z = 0
4 + y – z + y + 2z = 0
2y + z = -4
z = -4 – 2y… Jadilah persamaan (5)
Selanjutnya, silahkan subtitusikan persamaan keempat (4) ke persamaan ketiga (3).
- Sebelum: 3x + 2y + z = 2
- Sesudah: 3(4 + y – z) + 2y + z = 2
12 + 3y – 3z + 2y + z = 2
5y – 2z = -10… Jadilah persamaan (6)
Berikutnya subtitusikan persamaan kelima (5) ke persamaan keenam (6).
- Sebelum: 5y – 2z = -10
- Sesudah: 5y – 2(-4 – 2y) = -10
5y + 8 + 4y = -10
9y = -18
y = -18/9
y = -2 -> nilai y
Berikutnya Subtitusikan y = -2 ke persamaan kelima (5)
- Sebelum: z = -4 -2y
- Sesudah: z = -4 – 2(-2)
z = -4 – 4 = 0 -> nilai z
Subtitusikan y = -2 dan z = 0 ke persamaan keempat (4).
- Sebelum: x = 4 + y – z
- Sedudah: x = 4 +(-2) – 0
x = 4 – 2 = 2 -> nilai x
Dari soal SPLTV di atas nilai (x,y,z) berturut-turut adalah (2,-2,0).
2. Penyelesaian Soal SPLTV Metode Eliminasi
Penyelesaian SPLTV (dalam variabel x, y, dan z) dengan menggunakan metode eliminasi dapat dilakukan dengan langkah-langkah berikut ini.
- Eliminasi salah satu variabel baik x atau y atau z sehingga dapat diperoleh SPLDV (Sistem Persamaan Linear Dua Variabel).
- Selesaikan SPLDV pada langkah pertama dengan mengeliminasi variabel kedua supaya mendapatkan nilai variabel ketiga atau bisa juga dengan mengeliminasi variabel ketiga supaya mendapatkan nilai variabel kedua.
- Silahkan ulangi langkah pertama dan kedua dengan pemilihan variabel berbeda sampai mendapatkan nilai dari ketiga variabel tersebut.
Agar langkah-langkah di atas dapat lebih mudah dipahami, maka berikut contoh soal dari penyelesaian SPLTV dengan menggunakan metode Eliminasi.
x + y + 2z = 9 (Contoh Bentuk Persamaan 1)
2x + 4y – 3z = 1 (Contoh Bentuk Persamaan 2)
3x + 6y – 5z = 0 (Contoh Bentuk Persamaan 3)
Jawabannya:
- Eliminasi z dari persamaan pertama (1) dan kedua (2) sehingga dapat diperoleh.
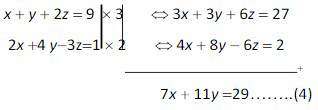
- Eliminasi z dari persamaan kedua (2) dan ketiga (3) sehingga dapat diperoleh.
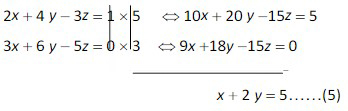
- Eliminasi x dari persamaan keempat (4) dan kelima (5) sehingga diperoleh.
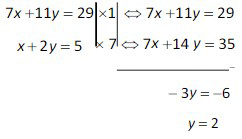
- Eliminasi y dari persamaan keempat (4) dan kelima (5) sehingga diperoleh.
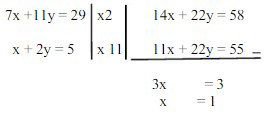
- Eliminasi y dari persamaan pertama (1) dan kedua (2) sehingga dapat diperoleh.
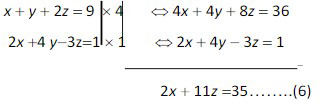
- Eliminasi y dari persamaan kedua (2) dan ketiga (3) sehingga dapat diperoleh.
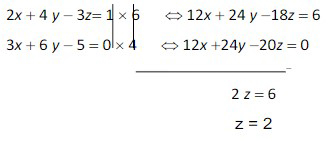
Dari soal SPLTV di atas nilai (x,y,z) berturut-turut adalah (1,2,2).
3. Penyelesaian Soal SPLTV Metode Gabungan (Campuran)
Penyelesaian SPLTV (dalam variabel x, y, dan z) dengan menggunakan metode gabungan atau campuran merupakan kombinasi 2 metode sebelumnya. Agar dapat lebih mudah dipahami, maka berikut contoh soal dari penyelesaian SPLTV dengan menggunakan metode Gabungan (Campuran).
x + y + 2z = 9 (Contoh Bentuk Persamaan 1)
2x + 4y – 3z = 1 (Contoh Bentuk Persamaan 2)
3x + 6y – 5z = 0 (Contoh Bentuk Persamaan 3)
Jawabannya:
- Eliminasi z dari persamaan pertama (1) dan kedua (2) sehingga dapat diperoleh.
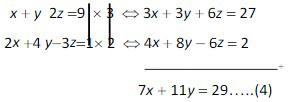
- Eliminasi z dari persamaan kedua (2) dan ketiga (3) sehingga dapat diperoleh.
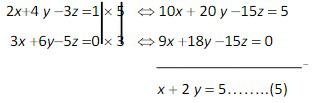
- Eliminasi x dari persamaan keempat (4) dan kelima (5) sehingga diperoleh.
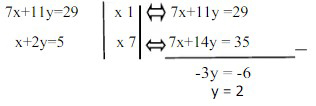
- Subtitusi y = 2 ke persamaan kelima (5) sehingga dapat diperoleh.
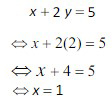
- Subtitusi y = 2 dan x = 1 ke persamaan pertama (1) sehingga diperoleh.
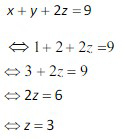
Dari soal SPLTV di atas nilai (x,y,z) berturut-turut adalah (1,2,3).
Dengan menggunakan metode di atas, maka contoh soal sesulit apapun bisa kalian jawab. Namun tetap dibutuhkan latihan dan belajar agar materi SPLTV ini dapat dipahami. Silahkan kerjakan semua contoh soal beserta perhitungannya tanpa melihat jawabannya terlebih dahulu.
Contoh Soal Singkat SPLTV Beserta Jawabannya
Supaya lebih mudah dalam memahami SPLTV ini, maka kita akan belajar melalui contoh soal singkat. Beberapa contoh soal dalam pembahasan ini juga sudah dituliskan beserta jawabannya. Namun perlu diingat untuk mengerjakan secara mandiri sebelum melihat jawabannya.
Berikut beberapa contoh soal singkat mengenai SPLTV beserta jawabannya.
1. Contoh Soal Singkat 1 Beserta Jawabannya
Tentukan himpunan penyelesaian dari SPLTV berikut ini.
5x – 3y + 2z = 3…. (Persamaan 1)
8x – 5y + 6z = 7…. (Persamaan 2)
3x + 4y – 3z = 15.. (Persamaan 3)
Jawabannya:
- Lakukan Proses Eliminasi

- Lakukan Proses Subtitusi

2. Contoh Soal Singkat 2 Beserta Jawabannya
Tentukan himpunan penyelesaian dari SPLTV berikut ini.
2x + 1y + 1z = 4….. (Persamaan 1)
3x – 1y + 2z =-5…. (Persamaan 2)
1x + 2y + 2z = 5….. (Persamaan 3)
Jawabannya:


Contoh Soal Cerita SPLTV Beserta Jawabannya dalam Kehidupan Sehari-hari
Selain contoh soal singkat beserta jawabannya, kita juga dapat berlatih dengan beberapa soal cerita. Tentunya dengan adanya contoh soal SPLTV dalam bentuk cerita, maka kita bisa mengetahui kegunaannya dalam kehidupan sehari-hari.
Berikut beberapa contoh soal cerita mengenai SPLTV beserta jawabannya.
1. Contoh Soal Cerita 1 Beserta Jawabannya
Ibu Darmono membeli 5kg telur, 2kg gula, dan 1kg tepung dengan harga Rp. 305.000,00. Ibu Juni membeli 3kg telur dan 1kg gula dengan harga Rp. 131.000,00. Ibu Ayu membeli 3kg gula dan 2kg tepung dengan harga Rp. 360.000,00.
Apabila Ibu Tebe membeli 3kg telur, 1kg gula, dan 2kg tepung, maka berapa harga belanjaan yang harus di bayarkan?
Jawabannya:
a. Variabel
- Harga Telur per Kg = x
- Harga Gula per Kg = y
- Harga Tepung per Kg = z
b. SPLTV
- Ibu Darmono : 5x + 2y + 1z = 305000… (Persamaan 1)
- Ibu Juni : 3x + 1y = 131000………….. (Persamaan 2)
- Ibu Ayu : 3y + 2z = 360000…………. (Persamaan 3)
Jadi SPLTV untuk Ibu Tebe adalah 3x + 1y + 2z.
Langkah Penyelesaian 1
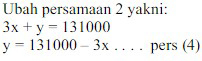
Langkah Penyelesaian 2

Langkah Penyelesaian 3

Langkah Penyelesaian 4

Langkah Penyelesaian 5

Langkah Penyelesaian 6
Jumlah harga yang harus dibayar Ibu Tebe yakni:
Ibu Tebe = 3x + y + 2z
Ibu Tebe = 3(17000) + 80000 + 2(60000)
Ibu Tebe = 51000 + 80000 + 120000
Ibu Tebe = 251000
Jadi, Ibu Tebe harus membayar seluruh belanjaan dengan harga Rp. 251.000,00.
2. Contoh Soal Cerita 2 Beserta Jawabannya
Dani, Umar, dan Beni ingin belanja kebutuhan sekolah pasca liburan. Dani membeli 3 Pensil, 4 Penghapus, dan 1 Buku Tulis. Umar membeli 6 Pensil, 2 Penghapus, dan 1 Buku Tulis. Sementara Beni membeli 2 Pensil, 5 Penghapus, dan 10 Buku Tulis.
Ketika berada di kasir, Dani harus membayar seharga Rp. 83.000,00. Umar harus membayar seharga Rp. 86.000,00. Sedangkan Beni harus membayar seharga Rp. 158.000,00. Berdasarkan keterangan tersebut, berapa harga dari masing-masing kebutuhan sekolah?
Jawabannya:
a. Variabel
- Harga Pensil = x
- Harga Penghapus = y
- Harga Buku Tulis = z
b. SPLTV
- Dani : 3x + 4y + 1z = 83000…….. (Persamaan 1)
- Umar : 6x + 2y + 1z = 86000…….. (Persamaan 2)
- Beni : 2x + 5y + 10z = 158000… (Persamaan 3)
c. Silahkan kerjakan soal di atas beserta langkah-langkahnya sebagai latihan!
Download Contoh Soal SPLTV (Sistem Persamaan Linear Tiga Variabel) PDF
Selain beberapa contoh soal SPLTV di atas, kami juga sudah merangkum beberapa contoh soal lainnya yang dapat digunakan sebagai sarana belajar. Semua soal tadi sudah terangkum dalam format PDF beserta jawabannya.
Agar dapat dijadikan sebagai bahan pembelajaran, berikut contoh soal SPLTV dalam bentuk PDF beserta jawabannya.
Akhir Kata
Melalui beberapa contoh soal SPLTV beserta jawabannya, kalian jadi lebih mudah memahami materi tersebut. Silahkan download contoh soal SPLTV PDF dalam pembahasan. Kerjakan secara mandiri beserta langkah-langkahnya, kemudian koreksi jawabannya.
Sekian pembahasan mengenai Soal SPLTV beserta Jawabannya dari Penulis Web Inspired2Write. Nantikan beragam contoh soal materi lain beserta jawabannya hanya dari kami. Semoga pembahasan ini bisa diterima oleh seluruh peserta didik maupun tenaga pendidik.
Sumber Gambar: Admin Inspired2Write, Buku.Kemdikbud.go.id, Nurul Rahmawati Spd, Muhammad Arif
