Contoh Soal Peluang Kejadian Majemuk – Pernahkah kamu bermain monopoli? Dalam bermain monopoli kamu harus melempar dadu bermata 6 untuk menghasilkan angka 1, 2, 3, 4, 5, atau 6. Kemungkinan keluarnya angka 6 pada pelemparan dadu adalah satu contoh peluang.
Contoh lainnya ialah ketika kami diminta untuk mengambil bola didalam keranjang secara acak. Peluang terambilnya bola warna merah dan biru kira-kira berapa? Kejadian-kejadian tersebut akan terjawab dengan mempelajari materi peluang kejadian majemuk dalam matematika.
Jika ada kejadian yang terjadi lebih dari satu kali, sehingga menghasilkan kejadian baru maka kejadian baru tersebut disebut dengan kejadian majemuk. Ada beberapa kejadian majemuk yang bisa kamu pelajari dalam teori peluang matematika yang akan kami bagikan berikut ini.
Dimana setelah mempelajari contoh soal mencari jarak pada peta, kini saatnya menambah ilmu tentang peluang kejadian majemuk mulai dari materi, rumus dan contoh soal. Adapun untuk ulasan lengkap terkait peluang kejadian majemuk dapat kamu simak melalui ulasan di bawah ini.
A. Peluang Kejadian Majemuk
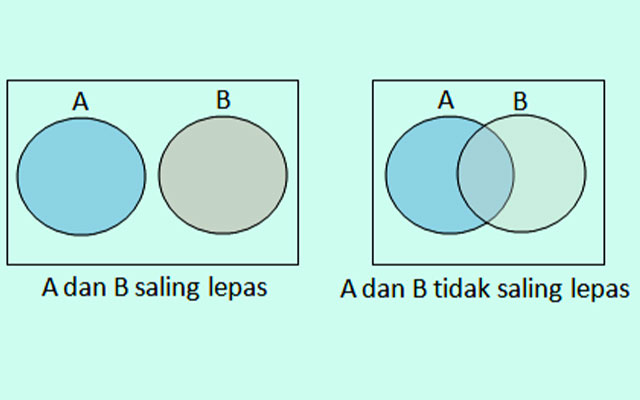
Peluang kejadian majemuk adalah peluang dengan kejadian yang terjadi lebih dari satu kali. Notasi untuk kejadian majemuk ialah ∪ (union). Misalnya A dan B merupakan dua kejadian dalam ruang sampel S, maka peluang kejadian dapat ditentukan dengan rumus berikut.
1. Peluang Kejadian Saling Tidak Lepas
Dua kejadian dikatakan tidak saling lepas bila ada minimal satu elemen pada kejadian A yang sama dengan elemen di kejadian B. Peluang salah satu A atau B dapat ditentukan dengan rumus.
P (A ∪ B) = P(A) + P(B) – P (A ∩ B)
Keterangan :
- P (A ∪ B) = Peluang terjadinya kejadian A atau B
- P(A) = Peluang terjadinya kejadian A
- P(B) = Peluang terjadinya kejadian B
- P (A ∩ B) = Peluang terjadinya kejadian A sekaligus B
Contoh Soal Peluang Kejadian Saling Tidak Lepas
| Dalam sebuah kelompok yang terdiri dari 30 siswa, ada 10 siswa suka matematika, 15 orang suka kimia dan 5 siswa lain suka kedua-duanya. Bila dipilih satu orang dari kelompok tersebut, tentukan peluang yang terpilih itu suka matematika atau fisika. Pembahasan : P (A ∪ B) = P(A) + P(B) – P (A ∩ B)  |
2. Peluang Kejadian Saling Lepas
Ada 2 kejadian yaitu A dan B disebut kejadian saling lepas, bila tidak ada elemen yang sama dari kedua kejadian tersebut. Peluang salah satu A atau B, mungkin terjadi kejadian saling lepas yang dapat ditentukan dengan rumus berikut ini.
P (A ∪ B) = P(A) + P(B)
Contoh Soal Peluang Kejadian Saling Lepas
| Pada percobaan pelamparan dadu dan uang logam, tentukan munculnya mata dadu < 3 dan mata dadu genap atau gambar? Pembahasan : a. Peluang munculnya mata dadu < 3 atau angka Ruang sampel pelemparan dadu = {1, 2, 3, 4, 5, 6} A = Kejadian munculnya dadu <3 P(A) = 2/3 = 1/2 Ruang sampel pelemparan uang logam = {A, G} B = Kejadian munculnya angka pada uang logam P(B) = 1/2 Dengan rumus peluang kejadian majemuk : P (A ∪ B) = P(A) + P(B) – P (A ∩ B) P (A ∩ B) = 0, maka :  b. Peluang munculnya mata dadu prima genap atau gambar Ruang sampel pelemparan dadu = {1, 2, 3, 4, 5, 6} A = Kejadian munculnya dadu <3 P(A) = 1/6 Ruang sampel pelemparan uang logam = {A, G} B = Kejadian munculnya angka pada uang logam P(B) = 1/2 Dengan rumus peluang kejadian majemuk : P (A ∪ B) = P(A) + P(B) – P (A ∩ B) P (A ∩ B) = 0, maka : 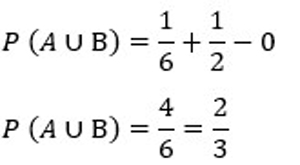 |
3. Peluang Saling Bebas
Dua kejadian A dan B dapat dikatakan saling bebas jika munculnya kejadian A tidak mempengaruhi kejadian B. Adapun rumus untuk menentukan kejadian saling bebas yaitu sebagai berikut :
P (A ∩ B) = P(A) × P(B)
Contoh Soal Peluang Saling Bebas
| Luffy melempar 2 buah dadu, berapakah peluang munculnya angka ganjil prima pada dadu pertama dan angka ganjil dadu kedua. Pembahasan : A = Peluang munculnya angka prima ganjil dadu 1 {3, 5} B = Peluang munculnya angka ganjil dadu 2 {1, 3, 5} P (A ∩ B) = P(A) × P(B) 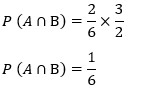 |
B. Peluang Kejadian Majemuk Bersyarat
Jika ada 2 kejadian A dan B dikatakan bersyarat apabila kejadian A mempengaruhi terjadinya kejadian B atau sebaliknya. Adapun rumus peluang kejadian majemuk bersyarat yaitu :
P (A ∩ B) = P(A) × P (B | A) atau P (A ∩ B) = P(B) × P (A | B)
Contoh Soal 4 :
| Sebuah keranjang berisi 5 bola merah dan 4 bola biru. Apabila diambil 2 buah bola satu persatu tanpa dikembalikan, tentukan peluang terambilnya bola merah berturut-turut. Penyelesaian : P(A) = Pengambilan bola merah pertama P(B) = Pengambilan bola merah kedua P(A) = 5/9 P(B) = 4/8 Peluang terambilnya bola merah yaitu : P (A ∩ B) = P(A) × P (B | A) 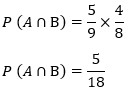 |
Contoh Soal 5 :
| Didalam kotak terdapat 6 bola merah dan 4 bola biru. Apabila diambil 2 buah bola satu persatu tanpa dikembalikan. Maka berapakah peluang bola merah terambil pada pengembalian pertama dan bola biru pada pengambilan kedua! Penyelesaian : Pada pengambilan pertama tersedia 5 bola merah dari 9 bola yang tersedia, maka P(M) = 6/10 Pada pengembalian kedua tersedia 4 bola biru dari 8 bola yang tersisa, maka P(M | K) = 5/9 Karena kejadian tersebut tidak saling mempengaruhi, maka : P (A ∩ B) = P(A) × P (B | A) 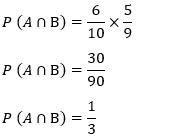 |
Contoh Soal Peluang Kejadian Majemuk

Nah, setelah mengetahui rumus peluang kejadian majemuk, berikut ada beberapa contoh soal peluang kejadian majemuk lainnya yang juga bisa kamu pelajari kembali. Selain contoh soal di atas, berikut contoh soal peluang kejadian majemuk berstandar HOST) beserta jawabannya.
Contoh Soal 6
| Sebuah dadu enam sisi dilemparkan satu kali, berapakah peluang munculnya dadu angka genap dan angka yang habis dibagi 3? Penyelesaian : Ruang sampel S = {1, 2, 3, 4, 5, 6} Misal A merupakan kejadian munculnya angka dadu genap dan B munculnya angka dadu yang habis dibagi tiga maka : A = {2, 4, 6}, B = {3, 6} dan A ∩ B = {1} Sehingga n(A) = 3, n(B) = 2, dan A ∩ B = 1 Maka : 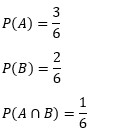 Jadi peluang kedua kejadian tersebut adalah P (A ∪ B) = P(A) + P(B) – P (A ∩ B) 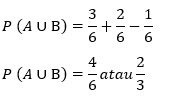 |
Contoh Soal 7
| Misalnya ketika memilih bola secara acak dari keranjang yang berisi 3 bola biru, 2 bola hijau dan 5 bola merah, peluang mendapat bola biru atau merah adalah …. Penyelesaian : P (Biru ∪ Merah) = P(Biru) + P (Merah)  |
Contoh Soal 8
| Ada dua kotak yang masing – masing memuat bola berwarna merah dan putih kotak I memuat 5 merah dan 4 putih serta kotak II memuat 6 merah dan 3 putih. Jika masing – masing kotak diambil 2 bola sekaligus, tentukan peluang terambilya 1 merah dan 1 putih pada kotak I dan 2 merah pada kotak II! Pembahasan : A adalah kejadian pada kotak I yaitu terambil 1M dan 1P, akan diambil dua bola sekaligus dari kotak I yang terdiri dari 9 bola Terpilih 1 merah dari 5 merah dan 1 putih dari 4 putih 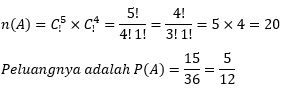 Misal B adalah kejadian pada kotak II yaitu terambil 2M akan diambil dua bola sekaligus dari kotak II yang terdiri dari 9 bola Terpilih 2 merah dari 6 merah 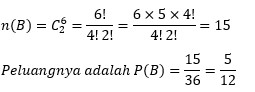 Maka peluang masing – masing kotak diambil 2 bola sekaligus, tentukan peluang terambilnya 1 merah dan 1 putih pada kotak I dan 2 merah pada kotak II merupakan kejadian saling bebas sehingga berlaku : P (A ∩ B) = P(A) × P(B) 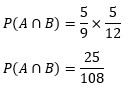 Jadi peluang kejadian A dan B adalah 25/108 |
Contoh Soal 9
| Sebuah dadu di lempar sekali tentukan peluang munculnya mata dadu genap dengan syarat munculnya kejadian mata dadu prima terlebih dahulu Penyelesaian : A adalah kejadian munculnya mata dadu prima Ruang sampel : S = {1,2,3,4,5,6}, sehingga 𝑛(𝑠) = 6 A = {2,3,5}, sehingga 𝑛(𝐴)= 3 Peluang kejadian A = P(A) = 3/6 atau 1/2 B adalah kejadian munculnya mata dadu genap B = {2,4,6), sehingga irisannya 𝐴 ∩ 𝐵 = {2}, dengan 𝑛(𝐴 ∩ 𝐵) = 1 Peluang kejadian P (A ∩ B) = 1/6 Jadi, peluang munculnya mata dadu genap dengan syarat munculnya kejadian mata dadu prima lebih dahulu 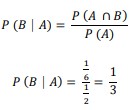 |
Contoh Soal 10
| Dalam pengocokan kartu remi, akan diambil dua kartu secara bersamaan yaitu kartu King berwarna merah atau kartu Jack. Berapa peluang kejadian tersebut? Penyelesaian : Diketahui: ruang sampel n(s) = 52 Ditanya : Peluang kejadian kartu King berwarna merah atau kartu Jack? Jawab : Jumlah kartu King berwarna merah ada 2 (King Heart dan King Diamond), sedangkan jumlah kartu Jack ada 4 (sebanyak jenis kartu). Maka:  |
Download Soal Peluang Kejadian Majemuk PDF
Nah, itulah sejumlah contoh soal peluang kejadian majemuk berbasis HOST. Nah, selain materi dan contoh soal di atas, berikut juga kami bagikan materi lengkap dan contoh soal peluang kejadian majemuk dalam format PDF yang dapat kamu unduh secara gratis melalui tautan berikut ini.
Demikianlah contoh soal peluang kejadian majemuk berbasis HOST beserta jawabannya yang dapat inspired2write.com sajikan untuk kamu pelajari dan pahami. Sekiranya cukup itu saja informasi dari kami, semoga artikel contoh soal di atas membantu kamu belajar.